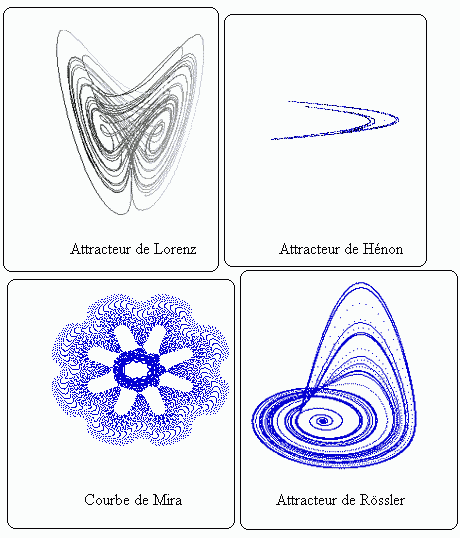

cliquez sur un des attracteurs pour l'agrandir
Les attracteurs étranges : L'attracteur étrange est une figure qui représente l'ensemble des trajectoires d'un système donné en proie à un mouvement chaotique. On peut définir l'attracteur étrange comme une carte des états imprévisibles et chaotiques; il révèle un ordre, une contrainte cachés, un "espace des phases" vers lequel convergent des phénomènes chaotiques. On pourrait comparer cet "espace des phases" à une vallée dont toutes les eaux ruisselantes convergeraient vers un cours d'eau unique. La nature fractale et les propriétés de l'attracteur étrange ont été découvertes en 1971 par David Ruelle et Floris Takens.